Geometri i praksis

Når vi tenker tilbake på matematikkundervisningen vi selv hadde går det samme igjen og igjen. Lærer som foreviser på tavla for deretter å sette oss elever i gang med oppgaver fra boka. Denne formen for undervisning opplevde vi som kjedelig og repeterende, det var liksom ikke spennende, interessant eller virkelighetsnært. Hvorfor ikke bruke nærmiljøet og alt spennende som finnes i og rundt skolen i geometriundervisningen?

Timms

TIMMS er en internasjonal studie i fagene matematikk og naturfag på grunnskolen. Testen gjennomføres hvert fjerde år, og presenterer data om elevers prestasjoner og læringsutbytte i matematikk og naturfag. TIMMS er også designet slik at en kan se utvikling av prestasjoner over tid, slik at en kan gjenkjenne positive eller negative indikatorer på hvordan utdanningssystemet fungerer (Bergem, Kaarstein, & Nilsen, 2016, s. 11) . Når det kommer til matematikk, kan en se at det er stor forskjell på hvordan norske elever på ungdomsskolen presterer. Det kommer frem at elevene presterer bra på emneområdene tall og statistikk, mens de presterer betydelig dårligere på områdene geometri og algebra. (Bergem, 2016, s. 36).

Vi anser det som spennende at norske elever skårer dårligere på geometri og algebra, og vil grunnet bloggens omfang fokusere på en av delene, nemlig geometri. Battista beskriver geometri som et nettverk av begreper, måter å forstå og representasjoner av systemer brukt til å utforske og analysere form og rom (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 260). Dette legger grunnlaget for vår oppgave med bakgrunn på hvordan elevene kan benytte seg av geometrien utenfor klasserommet og de tradisjonelle rammene for undervisningen.

Tett på realfag, nasjonal strategi for realfag i barnehagen og grunnopplæringen

Kunnskapsdepartementet opprettet såkalte realfagskommuner i prosjektet «tett på realfag, nasjonal strategi for realfag i barnehagen og grunnopplæringen». I dette prosjektet ble lærere, som jobbet med utforskende arbeid i matematikk, bedt om å svare på to spørsmål. Svarene på denne undersøkelsen av prosjektet, og spesielt svaret på et av spørsmålene som ble stilt, nemlig «Hvilke deler av matematikken kan være aktuell å arbeide med ute?» ga interessante svar (Gulaker & Reiten, 2018, ss. 181-182).

Figur 1: Gulaker & Reiten, 2018, ss.183

Ifølge Gulaker & Reiten viser undersøkelsen at det er mulig å jobbe med dette ute, noe som kan gi flere positive fordeler. De nevner blant annet at variasjon av undervisningen kan motivere flere elever til å lære matematikk, og at lærere lettere kan finne elevers riktige nivå ved å ta undervisningen med ut. Reikerås (Referert i Gulaker & Reiten, 2018, ss.183-184)  sier at barn har ulike kunnskapsspor, som betyr at elevene har ulik kunnskap og forskjellig utvikling frem til kunnskapen, noe som underbygger viktigheten av å jobbe med relasjonell matematikk. Om læreren styrer undervisningen fullstendig, vil de bli tvunget i et eksakt kunnskapsspor, som kan påvirke gleden ved matematikk negativt (Gulaker & Reiten, 2018, ss. 183-184).

Gulaker og Reiten henviser også til Væges undersøkelse, som skriver at det er tre forskjellige faktorer som påvirker elevenes følelse av kompetanse, autonomi og glede over å jobbe med matematikk. De er:
1. Undervisningsoppleggene gir utfordringer
2.Kan løses gjennom samarbeid
3. Arbeide med elevenes egne løsningsstrategier og metoder.
(Gulaker & Reiten, 2018, ss. 184-185)

Det å jobbe med utforskende undervisning vil derfor utfordre elevene ved å utforske egne interesser, og søke fellesskap for å finne løsningen på et problem. Det å jobbe undersøkende i matematikken, gjør at elevene kan tilegne seg en relasjonell matematikkforståelse, samt oppnå økt motivasjon for faget (Gulaker & Reiten, 2018, s. 185).

Van Hieles fem nivåer

Alle studenter/ elever kan utvikle ferdigheter innenfor tenkning og forståelse i geometriske kontekster, men denne ferdigheten krever pågående og betydelige erfaringer langs en utviklende progresjon (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 261). For å forklare setningen ovenfor på en god måte vil det være naturlig å trekke inn ekteparet Pierre van Hiele og Dina van Hiele-Geldof. De har laget et slags trappetrinns-system med forskjellige nivåer av geometrisk tenkning ut ifra hva elevene forstår. Van Hieles nivåer innenfor geometrisk tenkning har hatt stor innflytelse på matematikkundervisningen verden over (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 261). 

Figur 2: Van Hieles modell for forståelse i geometri. Bildet er hentet fra  https://ylgarris.wordpress.com/2013/07/15/the-van-hiele-levels-of-gemetric-understanding/

Figuren ovenfor viser de fem nivåene i Van Hieles modell for geometrisk tenkning. Studenter vil begynne på nivå 0 og gjennom erfaringer med geometri jobbe seg til neste nivå. Primært er elevene på mellomtrinnet på nivå 2, men ut ifra deres forutsetninger og ferdigheter kan det hende at elevene må jobbe både på nivå 0 og 1 fordi de ikke er klare for nivå 2 (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 261). 

Gjennom nivå 0 (Visualisering) skal elevene kunne gjenkjenne form på figurer og hva de ser ut som. En firkant er en firkant fordi den har fire hjørner. Samtidig kan et kvadrat snus slik at det ser ut som en diamant og elevene vil da se på figuren som en diamant. Man kan si at figurens opptreden er dominant og vil overvinne figurens form. Vektleggingen av nivå 0 er derfor på figurer og former som elevene kan observere, føle, bygge, ta del i eller jobbe med. Elevene skal prøve å se likheter og ulikheter mellom figurene og prøve å sette navn på figurene (eks: rektangel, kvadrat, rombe etc). Egenskapene til de forskjellige figurene (eks: parallelle sider, rette vinkler etc) er også inkludert men bare på en uformell måte (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 262 og 263). 

På nivå 1 (Analysering) skal elevene se helheten i stedet for den enkelte figur. Et konkret eksempel er at elevene ikke prater om et rektangel men alle rektangler. Elevene kan på dette nivået se at et rektangel har fire rette vinkler og to og to like lange sider. Det viktigste elevene sitter igjen med på nivå 1 er å se likheter mellom figurer med lik form og hva som kjennetegner dem (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 263). 

Når elevene er på nivå 2 (Uformell deduksjon) er elevene i stand til å se sammenhengen mellom egenskapene til geometriske figurer. De vil også kunne sammenligne forskjellige figurer og se ulike egenskaper som definerer dem. Et godt eksempel på dette er når alle vinkler i en firkant er like må det være et rektangel. Man kan videre si at observasjonene elevene gjør beveger seg forbi selve figuren og begrunnes gjennom logiske resonnementer om figurene. Elevene blir derfor i stand til å følge en uformell deduktiv argumentasjon om figurene og deres egenskaper (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 264).

Nivå 3 (Deduksjon) omhandler hvordan elevene analyserer uformelle argumenter. En elev på dette nivået er kapabel til å jobbe med abstrakte oppgaver om geometriske figurer og komme med konklusjoner basert på logikk (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 265). 

Nivå 4 (Stringens) er det høyeste i Van Hieles nivåer og det er sjelden man ser elever i grunnskolen på dette nivået. Her ligger oppmerksomheten i de aksiomatiske systemene og ikke bare i deduksjonen innenfor systemet. Hovedaspektet med dette nivåer er sammenligninger og kontraster rundt forskjellige aksiomatiske systemer innenfor geometrien (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 265). 

Relasjonell og instrumentell forståelse

Faux amis er et fransk begrep som beskriver to ord som er forholdsvis like på to forskjellige språk, der betydningen av ordet er annerledes. Et godt eksempel kan være det franske ordet «Libraire», som på engelsk betyr «Bookshop», og ikke «Library». En person som ikke er klar over at en bruker en såkalt «Faux amis» kan skape misforståelser i samfunnet. Du kan for eksempel låne en bok fra Biblioteket uten å betale, men de samme reglene gjelder ikke i en bokhandel. Ifølge Skemp kan vi finne såkalte «faux amis» i matematikkens verden, og det kan være roten til flere vansker i dagens matematikkundervisning (Skemp, 2006, ss. 88-89). 

En av disse feilene er forståelse, og Skemp er kjent for å snakke om to forskjellige typer forståelse, nemlig relasjonell og instrumentell forståelse. Skemp anerkjente ikke instrumentell forståelse som forståelse i starten, da han beskrev dette som «rules without reason». I ettertid har Skemp sett at besittelse av regelen, og evnen til å bruke den, kan anses som en forståelse (Skemp, 2006, s. 89). Det er et faktum at mange lærere underviser instrumentelt, og Skemp ser tre fordeler med å undervise på en slik måte: 

Figur 3: (Skemp, 2006, s. 92).  

Ifølge Skemp innebærer relasjonell forståelse at man vet både hva man skal gjøre og hvorfor en gjør det slik (Skemp, 2006, s. 89).  Skemp mener også at det er minst fire fordeler med å undervise mot relasjonell forståelse i klasserommet:

Figur 4:  (Skemp, 2006, ss. 92-93)

Sosiokulturelt læringssyn

I et sosiokulturelt syn på læring, kan en si at den som lærer er aktivt engasjert i å finne mening i læreprosessen, og i tillegg lære av noen med mer kunnskap. Alle elever har sin egen proksimale utviklingssone, som er et kunnskapsområde en elev ikke er i stand til å nå på egenhånd, men som er innen rekkevidde om de får hjelp av noen med mer kunnskap. Wood & Turner-Vorbeck (Referert i Van de Walle, Bay-Williams, Lovin & Karp, 2014, s.6) sier at elevenes forutsetninger for læring er størst når samtalen i klasserommet er innenfor den proksimale utviklingssonen til eleven/elevene. Om en klarer å holde samtalen innenfor denne sonen, vil elevene kanskje oppfatte undervisningen som mindre kjedelig. Wood & Turner sier også at klasseromsdiskusjoner som er basert på elevers egne ideer og løsningsforslag på problemer er fundamental for elevenes læring (Van de Walle, Bay-Williams, Lovin, & Karp, 2014, s. 6).

Uteskole

For at elevene virkelig skal sette pris på geometrien i naturen, som nevnes i kjerneelementet «matematiske kunnskapsområder» (Utdanningsdirektoratet, 2018) er det naturligvis viktig å ta elevene med ut i naturen. For å få mest mulig utbytte av uteskole, er det viktig at en har en plan og et formål for hva som skal læres i undervisningen. Det er viktig å tilpasse opplegget ut fra målgruppe, område, tidsrammen og innholdet. For å få til dette, kan det være lurt å koble opp undervisningen som skjer ute, med undervisningen som skjer inne. En av måtene for å få dette til er metoden forarbeid – uteaktiviteter – etterarbeid (Husby & Fiskum, 2014, s. 30).

Denne metoden består av en forberedelsesfase, gjennomføringsfase og til slutt en bearbeidingsfase. I forberedelsesfasen forbereder en seg på aktuell teori som er relevant for det en skal gjøre ute. Etterpå er gjennomføringsfasen, der en gjennomfører det planlagte opplegget. Dette kobler Husby og Fiskum (2014, s.31) opp mot Dewey, der hans tanker var at elevenes praktiske erfaringer skal kunne bidra til en økt forståelse av teoretiske emner. Til slutt er en bearbeidingsfase der elevene kan jobbe med logg og dokumentasjon fra turen (Husby & Fiskum, 2014, s. 31). 

Undervisningsopplegg 

I 2020 implementeres en ny læreplan i grunnskolen, og i forslaget til den nye læreplan nevnes nye kjerneelementer og kompetansemål som skal vektlegges/brukes i matematikkundervisningen.  I forslaget til ny læreplan, nevnes flere forskjellige kjerneelementer som er viktig for faget. Utforsking og problemløsning er et av kjerneelementene, og anses som det viktigste. De andre kjerneelementene må sees i sammenheng med dette elementet. Selve utforskingsdelen handler om at elevene skal lete etter mønster og finne sammenhenger. Det skal også legges mer vekt på ulike strategier og fremgangsmåter, fremfor selve løsningen. Et annet kjerneelement som nevner geometri konkret er kjerneelementet «matematiske kunnskapsområder». Dette sier at Geometri anses som viktig for elevene slik at de utvikler romforståelse, samt det å sette pris på geometrien i naturen og den menneskeskapte geometrien som blant annet finnes i kunst og arkitektur. Dette betyr blant annet at elevene skal utforske varierte former og figurer, slik at de skaffer seg innsikt i egenskaper og bruksområder, samt se eventuelle sammenhenger (Utdanningsdirektoratet, 2018).

På bakgrunn av dette vil vi legge til rette for et utforskende opplegg der elevene skal utforske og lete etter sammenhenger basert på Van Hieles nivå innenfor geometrisk tenking, der elevene oppsøker skolens uteområde for å se på den menneskeskapte geometrien i arkitekturen, samt utforske naturen og dens unike geometri. Undervisningsopplegget vi har laget er beregnet på en 9. klasse men kan lett omstruktureres og tilpasses til et lavere trinn eller motsatt

I og med at elevene skal oppsøke skolens uteområde for å utforske geometrien på skolens uteområde, er det viktig å koble sammen undervisningen som skjer ute, med undervisningen som foregår inne (Husby & Fiskum, 2014, s. 30). VI har valgt metoden forarbeid, uteaktiviteter og etterarbeid for å oppnå dette.  I dette undervisningsopplegget vil vi kun ta for oss uteaktiviteter og etterarbeidsfasen, og baserer opplegget på den forutsetning at elevene har gjennomført relevant geometriundervisning i forkant av uteaktivitetene. Dette er viktig å presisere, slik at elevene har gode forutsetninger for å løse vårt undervisningsopplegg som omhandler uteaktiviteter og en etterarbeidsfase.

Uteaktiviteter kalles ofte gjennomføringsfasen, og elevene får på dette tidspunktet utdelt oppgaver for dagens opplegg.

Figur 5: Oppgave 1

I oppgave 1 som elevene skal arbeide selvstendig med blir de utfordret til å se etter geometriske figurer/ gjenstander utenfor klasserommet. Her blir elevene utfordret til å tegne, navngi og forklare egenskapene til figurene. Dette kan knyttes direkte opp mot Van Hiele sine nivåer og brukes som et kartleggingsverktøy for hvor elevene befinner seg. Elevene blir også utfordret kreativt og må se på ting på en ny måte. Elever som ligger på nivå 0 og 1 vil kanskje klare å finne enkle figurer og navngi dem, mens elever på nivå 2 og 3 vil klare å finne mer komplekse gjenstander og beskrive kjennetegn ved dem. Etter den første oppgaven går elevene sammen i grupper og snakker om figurene de har funnet og hva som kjennetegner dem. Gjennom å oppsummere i grupper vil elevene få ideer videre når de skal gå i gang med oppgave 2 hvor de skal samarbeide. Dette tenker vi at også kan være en katalysator for de elevene som er på et lavere nivå ved at de kan bidra med forslag til figurer som de kan regne areal og volum av. Her vil også elevene på nivå 2 og 3 innta en slags mentorrolle for elevene på lavere nivå. Dette vil gi dem utfordringer gjennom å forklare og integrere de andre elevene i sine resonnementer og tankemåter. Dette kan knyttes opp mot den proksimale utviklingssonen der elevene kan strekke seg etter noe som er innenfor rekkevidde av hva de kan lære. Gjennom samtale mellom elevene og ikke en lærerstyrt oppsummering håper vi at elevene skal lære av hverandre og skape en motivasjon for oppgaven. Dette kan også ses i sammenheng med relasjonell forståelse hvor elevene må forklare og begrunne for hverandre. 

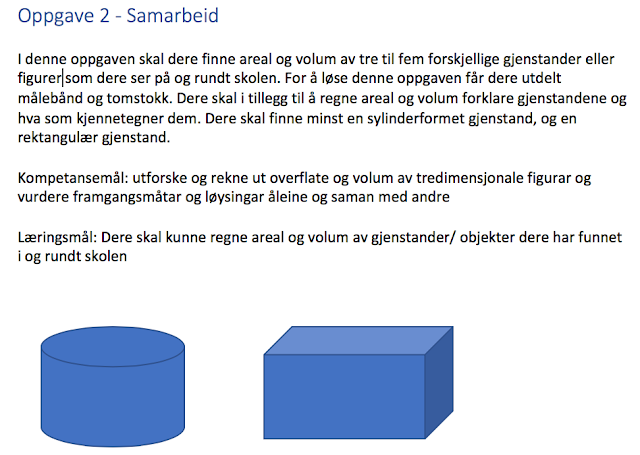Figur 6: Oppgave 2 (kompetansemål hentet fra: Utdanningsdirektoratet, 2018)

Når elevene går løs på oppgave 2 har de forhåpentligvis fått et solid grunnlag med ideer til hvordan den kan løses. I oppgave to kreves det at elevene har forståelse for hvordan man regner ut volum og areal. Selv om de kan ha en instrumentell forståelse gjennom bruk av formler tror vi at en slik oppgave kan være med på skape en relasjonell forståelse ved at de setter formlene ut i praksis og være med på å stimulere til økt romforståelse. Selv om noen elever kanskje ikke vil klare å regne ut volum kan de sitte igjen med en forståelse av hva volum er. Elever på nivå 2 og 3 vil også stimuleres ved at de kan finne andre spennende ting som de ønsker å finne svar på som for eksempel diagonaler (Se figur 8). Etter at elevene har funnet seg tre til fem figurer/ gjenstander og gjort det oppgaven ber dem om å gjøre tar man en muntlig oppsummering i klasserommet i fellesskap der elevene legger fram sine funn og argumenterer for dem. 

Figur 7: 

               

Figur 8:

Figur 9:

    

  

Figur 7,8 og 9 er eksempler som vi tror elevene kan finne og argumentere rundt gjennom å regne areal og volum samt beskrivelse av hva som kjennetegner de forskjellige gjenstandene.  

Til slutt kommer det en bearbeidingsfase, der Husby & Fiskum (2014, s. 31) anbefaler å jobbe med logg, dokumentasjon eller lignende. I vårt tilfelle føler vi at det ville være unaturlig å jobbe med logg eller dokumentasjon, men heller avslutte timen med en klasseromsbasert diskusjon basert på elevenes fremgangsmåter i gjennomføringsdelen, noe som Wood & Turner (referert i Van de Walle, Bay-Williams, Lovin & Karp, s.6) anså som fundamentalt for elevenes læring.

Konklusjon

Dette undervisningsopplegget er basert på Væges (Referert i Gulaker & Reiten, 2018, ss. 184-185) undersøkelse som nevner tre faktorer som påvirker elevenes følelse av kompetanse, autonomi og glede over å jobbe med matematikk. Den første faktoren er at undervisningsopplegget gir utfordringer. Vi har prøvd å tilpasse opplegget for alle elevene, ved å ha en åpen oppgave der elevene jobber på sitt nivå innenfor Van Hieles fem nivåer. Den andre faktoren er at det kan løses gjennom samarbeid. Vi har prøvd å legge til rette for samarbeid i oppgave to, ved at elevene jobber sammen i grupper. Oppgavene kan løses gjennom samarbeid, og det er mulig at de antatt svakere elevene får hjelp av de antatt sterkere elevene, slik at antatt svakere elevene kan lære og komme inn i sin proksimale utviklingssone. Når de sterkere elevene forklarer hvordan de løser en oppgave, stilles det større krav til en relasjonell forståelse og hvordan de løser den. Den siste faktoren er å arbeide med elevenes egne løsningsstrategier og metoder, noe som vi føler er delvis oppnådd med dette undervisningsopplegget. Elevene får til dels arbeide med egne løsningsstrategier og metoder i oppgavene. Kjerneelementet «matematiske kunnskapsområder» nevner at det er viktig for elevene å sette pris på geometrien i naturen og den menneskeskapte geometrien som finnes i kunst og arkitektur, og det var derfor naturlig å legge undervisningsopplegget i skolens nærområde. Det å jobbe ute vil også bidra til variasjon av undervisningen, som kan føre til at en treffer flere av elevenes kunnskapsspor, i og med at elevene har ulik kunnskap og forskjellig utvikling frem til kunnskapen. Dette underbygger viktigheten av å jobbe med relasjonell matematikk og vi satser på at undervisningsopplegget bidrar til at elevene får en tilfredsstillelse av å lære relasjonelt, slik at elevene blir som Skemps metafor, nemlig treet; der de kan utvide sine egne røtter innen matematikken.

Kandidat nr. 9 og 10.

Bibliografi

Bergem, O. K. (2016). Hovedresultater i matematikk. I O. K. Bergem, H. Kaarstein, & T. Nilsen, Vi kan lykkes i realfag: Resultater og analyser fra TIMMS 2015 (ss. 22-44). Universitetsforlaget.

Bergem, O. K., Kaarstein, H., & Nilsen, R. (2016). Vi kan lykkes i realfag: Resultater og analyser fra TIMMS 2015.Universitetsforlaget.

Gulaker, D., & Reiten, M. (2018). Hvordan skape motivasjon for matematikk. I T. A. Fiskum, D. Gulaker, & H. P. Andersen, Den engasjerte elevene: Undrende, utforskende og aktiviserende undervisning i skolen (ss. 169-187). Cappelen Damm Akademisk.

Husby, J., & Fiskum, T. (2014). Undervisningsmetoder ute og inne - den gode sammenhengen. I J. Husby, & T. Fiskum, Uteskoledidaktikk - Ta fagene med ut. Oslo: Cappelen Damm AS.

Skemp, R. R. (2006). Relational Understanding and Instrumental Understanding. Hentet fra https://www.jstor.org/stable/41182357?seq=1#metadata_info_tab_contents: https://www.jstor.org/stable/pdf/41182357.pdf?refreqid=excelsior%3Ad4fba55151cb027e300ddfc91fb0481f

Utdanningsdirektoratet. (2018, 10 18). Matematikk fellesfag. Hentet fra Utdanningsdirektoratet: https://hoering.udir.no/Hoering/v2/286?notatId=573&fbclid=IwAR1jfEdpiWBWUphK9DdEEP8lOOgwgBqvF8kOSJIiRTzEMgTgYPh7y6iutms

Van de Walle, J., Bay-Williams, J. M., Lovin, L. H., & Karp, K. S. (2014). Teaching Student-Centered Mathematics. Upper Saddle River: Pearson Education Inc.

https://ylgarris.wordpress.com/2013/07/15/the-van-hiele-levels-of-gemetric-understanding/